What you expect is what you get
This is a bit of a road-map essay, you can skip it without losing much.
Overview
This post refers to where we’d like umx to end up: As an intelligent research assistant: asking when you are unclear, but also able to understand your intentions.
Ideally it would be like Palantir ☺
Assisting requires taking an intentional stance. This is hard, and can lead to black-box behavior, so, read on.
The umx philosophy is “no black boxes”.
Unlike, say, Mplus, umx doesn’t do things behind the scenes. You get what you request: Nothing less, and nothing more (that said, umxRAM supports lavaan syntax, which gives access to scripts written in that language).
Partly the umx philosophy is aided by R - it makes function defaults transparent: When you omit arrows = 1, you can see (glass box) that mxPath is going to set arrows to 1, because that default is in the function definition.
Out of the box, the package umx builds on – OpenMx – requires explicit setting of many things you might “expect” to happen automagically. In particular, it doesn’t set start values or path labels. It also doesn’t add paths or objects you don’t explicitly request. So it doesn’t add residual variances or covariances among exogenous variables.
The goal of umx is to take a slightly different perspective, perhaps best phrased as “It’s easy to realise your expectations”.
umx is conservative in doing what you expect.
Things that go without saying…
What goes without saying? Let’s take the example of this model: What does it claim?
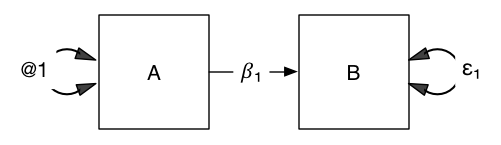
Most people would answer “A causes B”.
This however, leaves a lot of expectations implicit - a lot is “intended” to be understood.
Fully verbalized, people who know this means “changes in A cause changes in B” expect also that:
AandBare measured (squares)- That
AandBhave variance. - That
Aaccounts for some but not all of the variance inB. - But not all of it:
Bhas residual variance. - Variance of
Ais exogenous to the model.- The standardized variance of
Awill be 1.
- The standardized variance of
AandBhave means as well as variances.
How to implement this without black boxes? Let’s look at an lm statement of A -> B:
df = myFADataRaw[, 1:2]
names(df) <- c("A", "B")
summary(lm(B ~ A, data = df))
m1 = lm(B ~ A, data = df)
umxAPA(m1, std = TRUE)
# (Intercept) β = 0 [-0.07, 0.07], t = 0, p = 1.000
# A β = 0.63 [0.57, 0.7], t = 18.33, p < 0.001
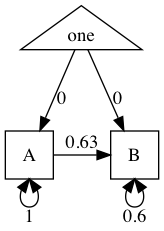
This tells us that B = A × 𝛽₁ + ε, where 𝛽₁ = 0.64 CI95[0.57, 0.71]. R² = 0.40 (F(1, 498) = 336.1, p-value: « .001)
Now in umx:
manifests = names(df)
m1 = umxRAM("A_causes_B", data = df, std= TRUE,
umxPath("A", to = "B"),
umxPath(var = manifests),
umxPath(means = manifests)
)
Fits well!
χ²(995) = 0, p = 1.000; CFI = 1; TLI = 1; RMSEA = 0
And gives the same parameters:
| name | Std.Estimate | Std.SE | CI |
|---|---|---|---|
| A to B | 0.63 | 0.03 | 0.63 [0.58, 0.69] |
| A with A | 1.00 | 0.00 | 1 [1, 1] |
| B with B | 0.60 | 0.03 | 0.6 [0.53, 0.66] |
tmx_show(m1)
plot(m1)
More complex ( and realistic) models…
This, more complex model is typical of real research (modified from Duncan, Haller, and Portes, 1968):
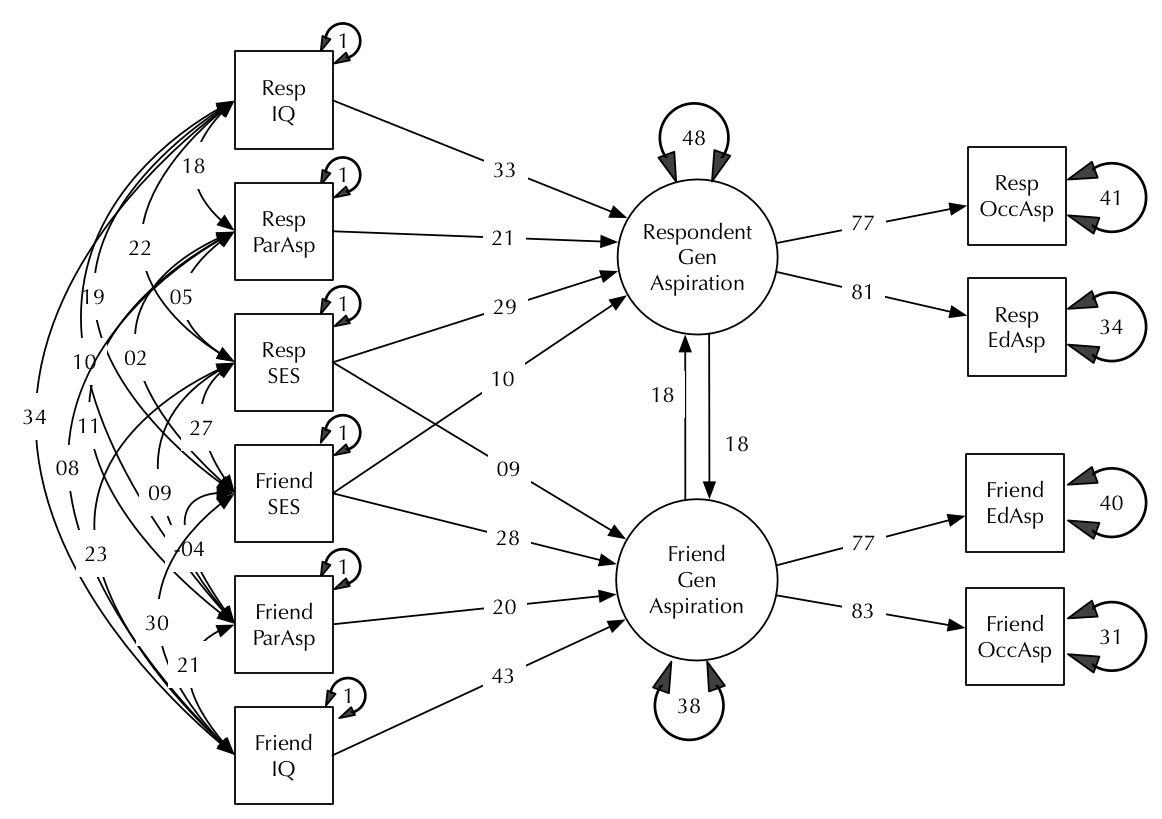
How would we state the claims of this model, and what do we expect an intelligent assistant to take taken for granted?
The theoretical claim is:
- Respondents and their friends each have a latent trait of “Aspiration”
- These are formed from their IQ, SES, and parental aspiration.
- SES effects impact on both respondent and friend’s aspiration.
- Latent aspiration affects occupational and educational aspiration.
- The aspiration latent traits have mutual influences on each other.
These four choices clearly will need to be specified by the researcher.
What can the assistant assume for any model? Clearly she can assume we intend this to be a RAM model if we are using umxRAM, She can also assume that anything in the data is manifest, and that anything not in the data is latent. She can assume that any variables in the data but never referred to in the model should be deleted. She should tell us about these assumptions and what they cause her to do.
That allows us to delete this code from a standard ram model:
type = "RAM"
latentVars = latents
manifestVars = manifests
Now some harder decisions. There are three claims of the model not yet included, for which our assistant might be able to assume intended answers.
- Should she assume that endogenous variables like occupational aspiration have residual variance?
- If so, we should automatically add:
umxPath(var = c(respondentAsp, friendAsp))- Some packages (
sem,lavaan, Mplus) implement this. We don’t: This a one-liner in umx, and adding it yourself keeps your thinking clear and explicit.
-
Should she assume that exogenous variables have variance?
umxPath(var = c(respondentFormants, friendFormants))- Again, this is easy to say with 1
umxPath, So auto-adding exogenous variances causes more mental work than it saves, IMHO.
- Again, this is easy to say with 1
- You need to set a scale for latent variables. Some users like to set the first loading on a factor to 1. Others fix the variance of latent traits @ 1. Should she assume one of these for us?
- My approach is to make it trivial to do this in the same umxPath statement that creates the loadings or the latent variance.
So you can say:
umxPath(var = "latentX", fixedAt = 1)
umxPath(means = "latentX", fixedAt = 0)
or
umxPath("latentX", to = c("DV1", "DV2", "DV3"), firstAt = 1) # fix the first path, leave the others free
You also have nifty short-cuts:
umxPath(v1m0 = "varName") # δ² = 1, mean = 0
umxPath(v0m0 = "varName") # δ² = 0, mean = 0
umxPath(v.m. = "varName") # δ² = free, mean = free
umxPath(v.m0 = "varName") # δ² = free, mean = 0
These shortcuts are equivalent too (but much easier to type and too read) two-line statements such as this:
mxPath("varName", free = FALSE, values = 1)
mxPath("one", to = "varName", free = FALSE, values = 0)
4th. Should she assume that exogenous variables all intercorrelate, and add this path automatically?
* umxRAM() could have the option covary.exogenous = FALSE. but again, who does this help when this is so clear?
umxPath(unique.bivariate = c(respondentFormants, friendFormants))
5th. Should she assume that latent traits like Respondent’s Aspiration have residual variance? * This seems wrong: The user can reasonably be expected to state this explicitly.
So then we would build this model in umx as follows.
First, let’s read in the Duncan data:
dimnames = c("RespOccAsp", "RespEduAsp", "FrndOccAsp", "FrndEduAsp", "RespParAsp", "RespIQ", "RespSES", "FrndSES", "FrndIQ", "FrndParAsp")
tmp = c(
c(0.6247,
0.3269, 0.3669,
0.4216, 0.3275, 0.6404,
0.2137, 0.2742, 0.1124, 0.0839,
0.4105, 0.4043, 0.2903, 0.2598, 0.1839,
0.3240, 0.4047, 0.3054, 0.2786, 0.0489, 0.2220,
0.2930, 0.2407, 0.4105, 0.3607, 0.0186, 0.1861, 0.2707,
0.2995, 0.2863, 0.5191, 0.5007, 0.0782, 0.3355, 0.2302, 0.2950,
0.0760, 0.0702, 0.2784, 0.1988, 0.1147, 0.1021, 0.0931, -0.0438, 0.2087)
)
duncan = umx_lower2full(tmp, diag = FALSE, dimnames = dimnames)
str(duncan)
duncan = mxData(duncan, type = "cov", numObs = 300)
And define some handy lists:
respondentFormants = c("RespSES", "FrndSES", "RespIQ", "RespParAsp")
friendFormants = c("FrndSES", "RespSES", "FrndIQ", "FrndParAsp")
respondentOutcomeAsp = c("RespOccAsp", "RespEduAsp")
friendOutcomeAsp = c("FrndOccAsp", "FrndEduAsp")
latentAspiration = c("RespLatentAsp", "FrndLatentAsp")
Now using these we can specify the model as follows:
m1 = umxRAM("Duncan", data = duncan,
# Working from the left of the model...
# Allow exogenous manifests to covary with each other
umxPath(unique.bivariate = c(friendFormants, respondentFormants)),
# Variance for the exogenous manifests (assumed error free)
umxPath(var = c(friendFormants, respondentFormants), fixedAt = 1),
# Paths from IQ, SES, and parental aspiration to latent aspiration, for Respondents
umxPath(respondentFormants, to = "RespLatentAsp"),
# And same for friends
umxPath(friendFormants, to = "FrndLatentAsp"),
# The two aspiration latent traits have residual variance.
umxPath(var = latentAspiration),
# And the latent traits each influence the other (equally)
umxPath(fromEach = latentAspiration, lbound = 0, ubound = 1), # Using one-label would equate these 2 influences
# Latent aspiration affects occupational and educational aspiration in respondents
umxPath("RespLatentAsp", to = respondentOutcomeAsp, firstAt = 1),
# umxPath("RespLatentAsp", to = respondentOutcomeAsp, labels = c("Asp_to_OccAsp", "Asp_to_EduAsp")),
# # And their friends
umxPath("FrndLatentAsp", to = friendOutcomeAsp, firstAt = 1),
# nb: The firstAt 1 provides scale to the latent variables
# (we could constrain the total variance of the latents to 1, but this is easy )
# Finally, on the right hand side of our envelope sketch, we've got
# residual variance for the endogenous manifests
umxPath(var = c(respondentOutcomeAsp, friendOutcomeAsp)),
autoRun = TRUE
)
plot(m1, std=T)
So: a smart, open, glass box, not a blackbox!
References
- Duncan OD, Haller AO, Portes A (1968). “Peer Influences on Aspirations: a Reinterpretation.” American Journal of Sociology, pp. 119–137.